I think the most correct way to describe utilisation of a hash-table is using chi-squared distributions and hypothesis and degrees of freedom and a bunch of other things nobody but an actuary remembers. So I was looking for a quick method that was close-enough but didn't require digging out a statistics text-book.
I'm sure I've re-invented some well-known measurement, but I'm not sure what it is. The idea is to add up the total steps required to look-up all elements in the hash-table, and compare that to the theoretical ideal of a uniformly balanced hash-table. You can then get a ratio that tells you if you're in the ball-park, or if you should try something else. A diagram should suffice.
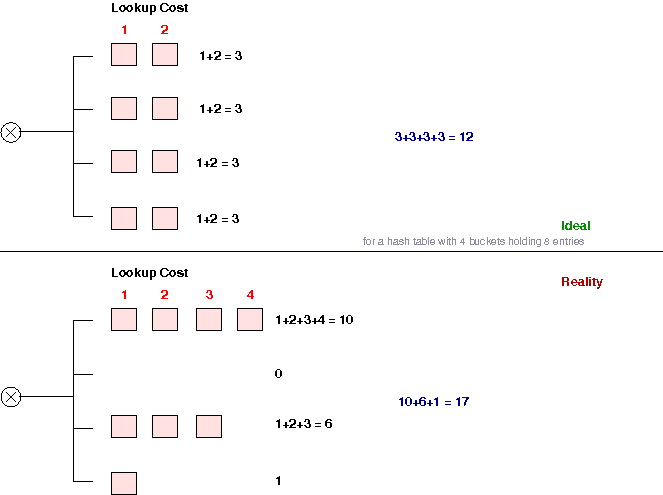
This seems to give quite useful results with a bare minimum of effort, and most importantly no tricky floating point math. For example, on the standard Unix words with a 2048 entry hash-table, the standard DJB hash came out very well (as expected)
Ideal 2408448 Actual 2473833 ---- Ratio 0.973569
To contrast, a simple "add each character" type hash:
Ideal 2408448 Actual 6367489 ---- Ratio 0.378241
Example code is hash-ratio.py. I expect this measurement is most useful when you have a largely static bunch of data for which you are attempting to choose an appropriate hash-function. I guess if you are really trying to hash more or less random incoming data and hence only have a random sample to work with, you can't avoid doing the "real" statistics.