I was at the airshow watching a C-17 Globemaster do its thing and the guy giving the spiel says how it is a completely fly-by-wire system, with quadruple redundancy. I thought to myself "that's a lot of redundancy" as it zoomed overhead.
As it happened, we were talking about the Byzantine generals on Thursday, and it finally sunk in.
The Byzantine Generals is a description of coming to consensus in a distributed system. The original paper gets pretty hairy, but the results are worth remembering.
The problem states there are a number of generals deciding if they should attack the enemy. Communication between the generals is considered secure (in the simplest case) but the alliance of all the generals is unknown. Loyal generals obviously tell the truth, but a dis-loyal general can either lie or tell the truth. A majority of the generals must concur; divided they can not defeat the enemy.
The implications for a distributed system are fairly clear. Reliable communication might be as simple as TCP/IP, and although computers aren't going to lie they may be faulty and not telling you the right thing. If that involves the difference between being above a mountain or flying into it, you want to be sure you get it right.
If there are just two of us, we can see that if one of us might be a traitor we can not decide on a course of action. If I say the height is 1000 feet and you say it is 2000 feet, there is no real way to decide who is right.
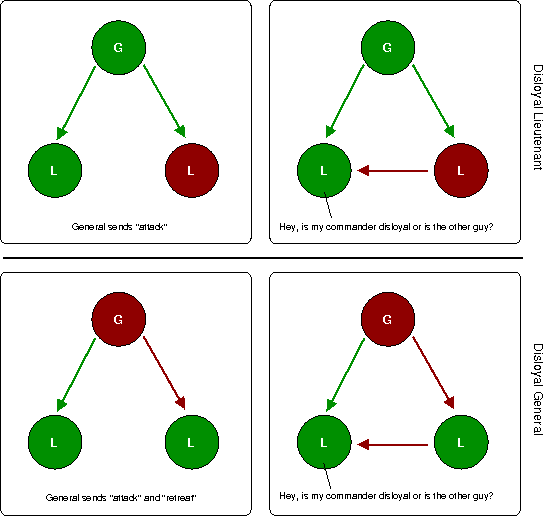
From the picture above, we can also see that if there are three of us, with one of us possibly disloyal, we can not ensure consistency. In the first case, the loyal general knows that one might be disloyal, but can't rely on the other lieutenant being loyal because he may have seen conflicting messages, and might go either way. So he can't be sure whether it will be an attack or retreat, so the situation is hopeless.
In the other case, the general is trying to confuse matters. He knows he is disloyal, so the other two are loyal. But this means he simply puts the system into an inconsistent state, where one lieutenant might go other way. Sounds a bit like something out of an episode of 24!
The paper shows that you can reduce all problems like this to some simple rules. It describes that to handle n faulty nodes, you require:
- 3n+1 working nodes
- 2n+1 independent communication channels
- n+1 rounds of communication
It turns out this is a real problem in real life and in real aeroplanes; the best paper I found was "The Real Byzantine Generals", Driscol, Hall, Paulitsch, Zumsteg, Digital Avionics Systems Conference, Salt Lake City, October 2004 (via IEEExpore if you have it). It mentions how the "anthropomorphic" basis for the problem may make many think they are immune to it, which is an interesting point.
So although 4 redundant systems sounds like a lot, it's just barely enough if you want the systems to have any sort of consensus.